2.9 Recursive Objects
Objects can have other objects as attribute values. When an object of some class has an attribute value of that same class, it is a recursive object.
2.9.1 Linked List Class
A linked list, introduced earlier in this chapter, is composed of a first element and the rest of the list. The rest of a linked list is itself a linked list — a recursive definition. The empty list is a special case of a linked list that has no first element or rest. A linked list is a sequence: it has a finite length and supports element selection by index.
We can now implement a class with the same behavior. In this version, we will define its behavior using special method names that allow our class to work with the built-in len function and element selection operator (square brackets or operator.getitem) in Python. These built-in functions invoke special method names of a class: length is computed by __len__ and element selection is computed by __getitem__. The empty linked list is represented by an empty tuple, which has length 0 and no elements.
>>> class Link:
"""A linked list with a first element and the rest."""
empty = ()
def __init__(self, first, rest=empty):
assert rest is Link.empty or isinstance(rest, Link)
self.first = first
self.rest = rest
def __getitem__(self, i):
if i == 0:
return self.first
else:
return self.rest[i-1]
def __len__(self):
return 1 + len(self.rest)
>>> s = Link(3, Link(4, Link(5)))
>>> len(s)
3
>>> s[1]
4
The definitions of __len__ and __getitem__ are in fact recursive. The built-in Python function len invokes a method called __len__ when applied to a user-defined object argument. Likewise, the element selection operator invokes a method called __getitem__. Thus, bodies of these two methods will call themselves indirectly. For __len__, the base case is reached when self.rest evaluates to the empty tuple, Link.empty, which has a length of 0.
The built-in isinstance function returns whether the first argument has a type that is or inherits from the second argument. isinstance(rest, Link) is true if rest is a Link instance or an instance of some sub-class of Link.
Our implementation is complete, but an instance of the Link class is currently difficult to inspect. To help with debugging, we can also define a function to convert a Link to a string expression.
>>> def link_expression(s):
"""Return a string that would evaluate to s."""
if s.rest is Link.empty:
rest = ''
else:
rest = ', ' + link_expression(s.rest)
return 'Link({0}{1})'.format(s.first, rest)
>>> link_expression(s)
'Link(3, Link(4, Link(5)))'
This way of displaying an Link is so convenient that we would like to use it whenever an Link instance is displayed. We can ensure this behavior by setting the link_expression function as the value of the special class attribute __repr__. Python displays instances of user-defined classes by invoking their __repr__ method.
>>> Link.__repr__ = link_expression
>>> s
Link(3, Link(4, Link(5)))
The Link class has the closure property. Just as an element of a list can itself be a list, a Link can contain a Link as its first element.
>>> s_first = Link(s, Link(6))
>>> s_first
Link(Link(3, Link(4, Link(5))), Link(6))
The s_first linked list has only two elements, but its first element is a linked list with three elements.
>>> len(s_first)
2
>>> len(s_first[0])
3
>>> s_first[0][2]
5
Recursive functions are particularly well-suited to manipulate linked lists. For instance, the recursive extend_link function builds a linked list containing the elements of one Link instance s followed by the elements of another Link instance t. Installing this function as the __add__ method of the Link class emulates the addition behavior of a built-in list.
>>> def extend_link(s, t):
if s is Link.empty:
return t
else:
return Link(s.first, extend_link(s.rest, t))
>>> extend_link(s, s)
Link(3, Link(4, Link(5, Link(3, Link(4, Link(5))))))
>>> Link.__add__ = extend_link
>>> s + s
Link(3, Link(4, Link(5, Link(3, Link(4, Link(5))))))
Rather than list comprehensions, one linked list can be generated from another using two higher-order functions: map_link and filter_link. The map_link function defined below applies a function f to each element of a linked list s and constructs a linked list containing the results.
>>> def map_link(f, s):
if s is Link.empty:
return s
else:
return Link(f(s.first), map_link(f, s.rest))
>>> map_link(square, s)
Link(9, Link(16, Link(25)))
The filter_link function returns a linked list containing all elements of a linked list s for which f returns a true value. The combination of map_link and filter_link can express the same logic as a list comprehension.
>>> def filter_link(f, s):
if s is Link.empty:
return s
else:
filtered = filter_link(f, s.rest)
if f(s.first):
return Link(s.first, filtered)
else:
return filtered
>>> odd = lambda x: x % 2 == 1
>>> map_link(square, filter_link(odd, s))
Link(9, Link(25))
>>> [square(x) for x in [3, 4, 5] if odd(x)]
[9, 25]
The join_link function recursively constructs a string that contains the elements of a linked list seperated by some separator string. The result is much more compact than the output of link_expression.
>>> def join_link(s, separator):
if s is Link.empty:
return ""
elif s.rest is Link.empty:
return str(s.first)
else:
return str(s.first) + separator + join_link(s.rest, separator)
>>> join_link(s, ", ")
'3, 4, 5'
Recursive Construction. Linked lists are particularly useful when constructing sequences incrementally, a situation that arises often in recursive computations.
The count_partitions function from Chapter 1 counted the number of ways to partition an integer n using parts up to size m via a tree-recursive process. With sequences, we can also enumerate these partitions explicitly using a similar process.
We follow the same recursive analysis of the problem as we did while counting: partitioning n using integers up to m involves either
- partitioning n-m using integers up to m, or
- partitioning n using integers up to m-1.
For base cases, we find that 0 has an empty partition, while partitioning a negative integer or using parts smaller than 1 is impossible.
>>> def partitions(n, m):
"""Return a linked list of partitions of n using parts of up to m.
Each partition is represented as a linked list.
"""
if n == 0:
return Link(Link.empty) # A list containing the empty partition
elif n < 0 or m == 0:
return Link.empty
else:
using_m = partitions(n-m, m)
with_m = map_link(lambda s: Link(m, s), using_m)
without_m = partitions(n, m-1)
return with_m + without_m
In the recursive case, we construct two sublists of partitions. The first uses m, and so we add m to each element of the result using_m to form with_m.
The result of partitions is highly nested: a linked list of linked lists. Using join_link with appropriate separators, we can display the partitions in a human-readable manner.
>>> def print_partitions(n, m):
lists = partitions(n, m)
strings = map_link(lambda s: join_link(s, " + "), lists)
print(join_link(strings, "\n"))
>>> print_partitions(6, 4)
4 + 2
4 + 1 + 1
3 + 3
3 + 2 + 1
3 + 1 + 1 + 1
2 + 2 + 2
2 + 2 + 1 + 1
2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1
2.9.2 Tree Class
Trees can also be represented by instances of user-defined classes, rather than nested instances of built-in sequence types. A tree is any data structure that has as an attribute a sequence of branches that are also trees.
Internal values. Previously, we defined trees in such a way that all values appeared at the leaves of the tree. It is also common to define trees that have internal values at the roots of each subtree. An internal value is called an label in the tree. The Tree class below represents such trees, in which each tree has a sequence of branches that are also trees.
>>> class Tree:
def __init__(self, label, branches=()):
self.label = label
for branch in branches:
assert isinstance(branch, Tree)
self.branches = branches
def __repr__(self):
if self.branches:
return 'Tree({0}, {1})'.format(self.label, repr(self.branches))
else:
return 'Tree({0})'.format(repr(self.label))
def is_leaf(self):
return not self.branches
The Tree class can represent, for instance, the values computed in an expression tree for the recursive implementation of fib, the function for computing Fibonacci numbers. The function fib_tree(n) below returns a Tree that has the nth Fibonacci number as its label and a trace of all previously computed Fibonacci numbers within its branches.
>>> def fib_tree(n):
if n == 1:
return Tree(0)
elif n == 2:
return Tree(1)
else:
left = fib_tree(n-2)
right = fib_tree(n-1)
return Tree(left.label + right.label, (left, right))
>>> fib_tree(5)
Tree(3, (Tree(1, (Tree(0), Tree(1))), Tree(2, (Tree(1), Tree(1, (Tree(0), Tree(1)))))))
Trees represented in this way are also processed using recursive functions. For example, we can sum the labels of a tree. As a base case, we return that an empty branch has no labels.
>>> def sum_labels(t):
"""Sum the labels of a Tree instance, which may be None."""
return t.label + sum([sum_labels(b) for b in t.branches])
>>> sum_labels(fib_tree(5))
10
We can also apply memo to construct a Fibonacci tree, where repeated subtrees are only created once by the memoized version of fib_tree, but are used multiple times as branches of different larger trees.
>>> fib_tree = memo(fib_tree)
>>> big_fib_tree = fib_tree(35)
>>> big_fib_tree.label
5702887
>>> big_fib_tree.branches[0] is big_fib_tree.branches[1].branches[1]
True
>>> sum_labels = memo(sum_labels)
>>> sum_labels(big_fib_tree)
142587180
The amount of computation time and memory saved by memoization in these cases is substantial. Instead of creating 18,454,929 different instances of the Tree class, we now create only 35.
2.9.3 Sets
In addition to the list, tuple, and dictionary, Python has a fourth built-in container type called a set. Set literals follow the mathematical notation of elements enclosed in braces. Duplicate elements are removed upon construction. Sets are unordered collections, and so the printed ordering may differ from the element ordering in the set literal.
>>> s = {3, 2, 1, 4, 4}
>>> s
{1, 2, 3, 4}
Python sets support a variety of operations, including membership tests, length computation, and the standard set operations of union and intersection
>>> 3 in s
True
>>> len(s)
4
>>> s.union({1, 5})
{1, 2, 3, 4, 5}
>>> s.intersection({6, 5, 4, 3})
{3, 4}
In addition to union and intersection, Python sets support several other methods. The predicates isdisjoint, issubset, and issuperset provide set comparison. Sets are mutable, and can be changed one element at a time using add, remove, discard, and pop. Additional methods provide multi-element mutations, such as clear and update. The Python documentation for sets should be sufficiently intelligible at this point of the course to fill in the details.
Implementing sets. Abstractly, a set is a collection of distinct objects that supports membership testing, union, intersection, and adjunction. Adjoining an element and a set returns a new set that contains all of the original set's elements along with the new element, if it is distinct. Union and intersection return the set of elements that appear in either or both sets, respectively. As with any data abstraction, we are free to implement any functions over any representation of sets that provides this collection of behaviors.
In the remainder of this section, we consider three different methods of implementing sets that vary in their representation. We will characterize the efficiency of these different representations by analyzing the order of growth of set operations. We will use our Link and Tree classes from earlier in this section, which allow for simple and elegant recursive solutions for elementary set operations.
Sets as unordered sequences. One way to represent a set is as a sequence in which no element appears more than once. The empty set is represented by the empty sequence. Membership testing walks recursively through the list.
>>> def empty(s):
return s is Link.empty
>>> def set_contains(s, v):
"""Return True if and only if set s contains v."""
if empty(s):
return False
elif s.first == v:
return True
else:
return set_contains(s.rest, v)
>>> s = Link(4, Link(1, Link(5)))
>>> set_contains(s, 2)
False
>>> set_contains(s, 5)
True
This implementation of set_contains requires $\Theta(n)$ time on average to test membership of an element, where $n$ is the size of the set s. Using this linear-time function for membership, we can adjoin an element to a set, also in linear time.
>>> def adjoin_set(s, v):
"""Return a set containing all elements of s and element v."""
if set_contains(s, v):
return s
else:
return Link(v, s)
>>> t = adjoin_set(s, 2)
>>> t
Link(2, Link(4, Link(1, Link(5))))
In designing a representation, one of the issues with which we should be concerned is efficiency. Intersecting two sets set1 and set2 also requires membership testing, but this time each element of set1 must be tested for membership in set2, leading to a quadratic order of growth in the number of steps, $\Theta(n^2)$, for two sets of size $n$.
>>> def intersect_set(set1, set2):
"""Return a set containing all elements common to set1 and set2."""
return keep_if_link(set1, lambda v: set_contains(set2, v))
>>> intersect_set(t, apply_to_all_link(s, square))
Link(4, Link(1))
When computing the union of two sets, we must be careful not to include any element twice. The union_set function also requires a linear number of membership tests, creating a process that also includes $\Theta(n^2)$ steps.
>>> def union_set(set1, set2):
"""Return a set containing all elements either in set1 or set2."""
set1_not_set2 = keep_if_link(set1, lambda v: not set_contains(set2, v))
return extend_link(set1_not_set2, set2)
>>> union_set(t, s)
Link(2, Link(4, Link(1, Link(5))))
Sets as ordered sequences. One way to speed up our set operations is to change the representation so that the set elements are listed in increasing order. To do this, we need some way to compare two objects so that we can say which is bigger. In Python, many different types of objects can be compared using < and > operators, but we will concentrate on numbers in this example. We will represent a set of numbers by listing its elements in increasing order.
One advantage of ordering shows up in set_contains: In checking for the presence of an object, we no longer have to scan the entire set. If we reach a set element that is larger than the item we are looking for, then we know that the item is not in the set:
>>> def set_contains(s, v):
if empty(s) or s.first > v:
return False
elif s.first == v:
return True
else:
return set_contains(s.rest, v)
>>> u = Link(1, Link(4, Link(5)))
>>> set_contains(u, 0)
False
>>> set_contains(u, 4)
True
How many steps does this save? In the worst case, the item we are looking for may be the largest one in the set, so the number of steps is the same as for the unordered representation. On the other hand, if we search for items of many different sizes we can expect that sometimes we will be able to stop searching at a point near the beginning of the list and that other times we will still need to examine most of the list. On average we should expect to have to examine about half of the items in the set. Thus, the average number of steps required will be about $\frac{n}{2}$. This is still $\Theta(n)$ growth, but it does save us some time in practice over the previous implementation.
We can obtain a more impressive speedup by re-implementing intersect_set. In the unordered representation, this operation required $\Theta(n^2)$ steps because we performed a complete scan of set2 for each element of set1. But with the ordered representation, we can use a more clever method. We iterate through both sets simultaneously, tracking an element e1 in set1 and e2 in set2. When e1 and e2 are equal, we include that element in the intersection.
Suppose, however, that e1 is less than e2. Since e2 is smaller than the remaining elements of set2, we can immediately conclude that e1 cannot appear anywhere in the remainder of set2 and hence is not in the intersection. Thus, we no longer need to consider e1; we discard it and proceed to the next element of set1. Similar logic advances through the elements of set2 when e2 < e1. Here is the function:
>>> def intersect_set(set1, set2):
if empty(set1) or empty(set2):
return Link.empty
else:
e1, e2 = set1.first, set2.first
if e1 == e2:
return Link(e1, intersect_set(set1.rest, set2.rest))
elif e1 < e2:
return intersect_set(set1.rest, set2)
elif e2 < e1:
return intersect_set(set1, set2.rest)
>>> intersect_set(s, s.rest)
Link(4, Link(5))
To estimate the number of steps required by this process, observe that in each step we shrink the size of at least one of the sets. Thus, the number of steps required is at most the sum of the sizes of set1 and set2, rather than the product of the sizes, as with the unordered representation. This is $\Theta(n)$ growth rather than $\Theta(n^2)$ -- a considerable speedup, even for sets of moderate size. For example, the intersection of two sets of size 100 will take around 200 steps, rather than 10,000 for the unordered representation.
Adjunction and union for sets represented as ordered sequences can also be computed in linear time. These implementations are left as an exercise.
Sets as binary search trees. We can do better than the ordered-list representation by arranging the set elements in the form of a tree with exactly two branches. The entry of the root of the tree holds one element of the set. The entries within the left branch include all elements smaller than the one at the root. Entries in the right branch include all elements greater than the one at the root. The figure below shows some trees that represent the set {1, 3, 5, 7, 9, 11}. The same set may be represented by a tree in a number of different ways. In all binary search trees, all elements in the left branch be smaller than the entry at the root, and that all elements in the right subtree be larger.
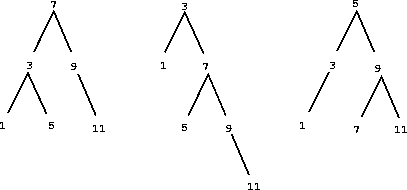
The advantage of the tree representation is this: Suppose we want to check whether a value v is contained in a set. We begin by comparing v with entry. If v is less than this, we know that we need only search the left subtree; if v is greater, we need only search the right subtree. Now, if the tree is "balanced," each of these subtrees will be about half the size of the original. Thus, in one step we have reduced the problem of searching a tree of size $n$ to searching a tree of size $\frac{n}{2}$. Since the size of the tree is halved at each step, we should expect that the number of steps needed to search a tree grows as $\Theta(\log n)$. For large sets, this will be a significant speedup over the previous representations. This set_contains function exploits the ordering structure of the tree-structured set.
>>> def set_contains(s, v):
if s is None:
return False
elif s.entry == v:
return True
elif s.entry < v:
return set_contains(s.right, v)
elif s.entry > v:
return set_contains(s.left, v)
Adjoining an item to a set is implemented similarly and also requires $\Theta(\log n)$ steps. To adjoin a value v, we compare v with entry to determine whether v should be added to the right or to the left branch, and having adjoined v to the appropriate branch we piece this newly constructed branch together with the original entry and the other branch. If v is equal to the entry, we just return the node. If we are asked to adjoin v to an empty tree, we generate a Tree that has v as the entry and empty right and left branches. Here is the function:
>>> def adjoin_set(s, v):
if s is None:
return Tree(v)
elif s.entry == v:
return s
elif s.entry < v:
return Tree(s.entry, s.left, adjoin_set(s.right, v))
elif s.entry > v:
return Tree(s.entry, adjoin_set(s.left, v), s.right)
>>> adjoin_set(adjoin_set(adjoin_set(None, 2), 3), 1)
Tree(2, Tree(1), Tree(3))
Our claim that searching the tree can be performed in a logarithmic number of steps rests on the assumption that the tree is "balanced," i.e., that the left and the right subtree of every tree have approximately the same number of elements, so that each subtree contains about half the elements of its parent. But how can we be certain that the trees we construct will be balanced? Even if we start with a balanced tree, adding elements with adjoin_set may produce an unbalanced result. Since the position of a newly adjoined element depends on how the element compares with the items already in the set, we can expect that if we add elements "randomly" the tree will tend to be balanced on the average.
But this is not a guarantee. For example, if we start with an empty set and adjoin the numbers 1 through 7 in sequence we end up with a highly unbalanced tree in which all the left subtrees are empty, so it has no advantage over a simple ordered list. One way to solve this problem is to define an operation that transforms an arbitrary tree into a balanced tree with the same elements. We can perform this transformation after every few adjoin_set operations to keep our set in balance.
Intersection and union operations can be performed on tree-structured sets in linear time by converting them to ordered lists and back. The details are left as an exercise.
Python set implementation. The set type that is built into Python does not use any of these representations internally. Instead, Python uses a representation that gives constant-time membership tests and adjoin operations based on a technique called hashing, which is a topic for another course. Built-in Python sets cannot contain mutable data types, such as lists, dictionaries, or other sets. To allow for nested sets, Python also includes a built-in immutable frozenset class that shares methods with the set class but excludes mutation methods and operators.